Concepts#
This block is about how we pull off the trick to turn geography into numbers statistics can understand. At this point, we dive right into the more methodological part of the course; so you can expect a bit of a ramp up in the conceptual sections. Take a deep breath and jump in, it’s well worth the effort! At the same time, the coding side of each block will start looking more and more familiar because we are starting to repeat concepts and we will introduce less new building blocks and instead rely more and more on what we have seen, just adding small bits here and there.
Space, formally#
How do you express geographical relations between objects (e.g. areas, points) in a way that can be used in statistical analysis? This is exactly the core of what we get into in here. There are several ways, of course, but one of the most widespread approaches is what is termed spatial weights matrices. We motivate their role and define them in the following clip.
Once you have watched the clip above, here’s a quiz for you!
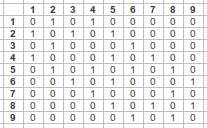
Imagine a geography of squared regions (ie. a grid) with the following structure:
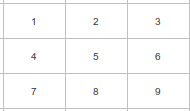
Each region is assigned an ID; so the most north-west region is 1, while the most south-east is 9. Here’s a question:
What is the dimension of the Spatial Weights Matrix for the region above?
Tip
It is one of the following:
\(3 \times 3\)
\(9 \times 3\)
\(3 \times 9\)
\(9 \times 9\)
Solution
It is nine rows by nine columns. To see why, remember that spatial weights matrices are \(N \times N\), as they need to record the spatial relationship between every single observation (regions in the example above), with every other single observation on the dataset.
Types of Weights#
Once we know what spatial weights are generally, in this clip we dive into some of the specific types we can build for our analyses.
Here is a second question for you once you have watched the clip above:
What does the rook contiguity spatial weights matrix look like for the region abvoe? Can you write it down by hand?
The Spatial Lag#
We wrap up the the set of concepts in this block with one of the applications that makes spatial weights matrices so important: the spatial lag. Watch the clip to find out what it is and then jump over the next part to see how all of these ideas translate into delicious, juicy Python code!
More materials#
If you want a similar but slightly different take on spatial weights by Luc Anselin, one of the biggest minds in the field of spatial analysis, I strongly recommend you watch the following two clips, part of the course offered by the Spatial Data Center at the University of Chicago:
Lecture on “Spatial Weights”
Show code cell outputs
Lecture on “Spatial Lag”, you can ignore the last five minutes as they are a bit more advanced
Show code cell outputs
Further readings#
If you liked what you saw in this section and would like to digg deeper into spatial weights, the following readings are good next steps:
Spatial weights chapter on the GDS book (in progress) reyABwolf.
For a more advanced and detailed treatment, the chapters on spatial weights in the Anselin & Rey book anselin2014modern are the best source.