.ipynb .pdf

Binder

Contents

Geovisualisation

📖 Ahead of time…

This block is all about visualising statistical data on top of a geography. Although this task looks simple, there are a few technical and conceptual building blocks that it helps to understand before we try to make our own maps. Aim to complete the following readings by the time we get our hands on the keyboard:

• Block D of the GDS course [AB19], which provides an introduction to choropleths (statistical maps)

• Chapter 5 of the GDS Book [RABWng], discussing choropleths in more detail

💻 Hands-on coding

import geopandas
import xarray, rioxarray
import contextily
import seaborn as sns
from pysal.viz import mapclassify as mc
from legendgram import legendgram
import matplotlib.pyplot as plt
import palettable.matplotlib as palmpl
from splot.mapping import vba_choropleth

Data

Data

If you want to read more about the data sources behind this dataset, head to the Datasets section

Local files

Assuming you have the file locally on the path ../data/:

db = geopandas.read_file("../data/cambodia_regional.gpkg")

Online read

If you’re online, you can do:

db = geopandas.read_file(
    "https://darribas.org/gds4ae/_downloads/9366d230310a8a68b2ce6cf2787a2f1c/cambodia_regional.gpkg"
)

ax = db.to_crs(
    epsg=3857
).plot(
    edgecolor="red",
    facecolor="none",
    linewidth=2,
    alpha=0.25,
    figsize=(9, 9)
)
contextily.add_basemap(
    ax,
    source=contextily.providers.Esri.NatGeoWorldMap
)
ax.set_axis_off();

db.info()

<class 'geopandas.geodataframe.GeoDataFrame'>
RangeIndex: 198 entries, 0 to 197
Data columns (total 6 columns):
 #   Column      Non-Null Count  Dtype   
---  ------      --------------  -----   
 0   adm2_name   198 non-null    object  
 1   adm2_altnm  122 non-null    object  
 2   motor_mean  198 non-null    float64 
 3   walk_mean   198 non-null    float64 
 4   no2_mean    198 non-null    float64 
 5   geometry    198 non-null    geometry
dtypes: float64(3), geometry(1), object(2)
memory usage: 9.4+ KB

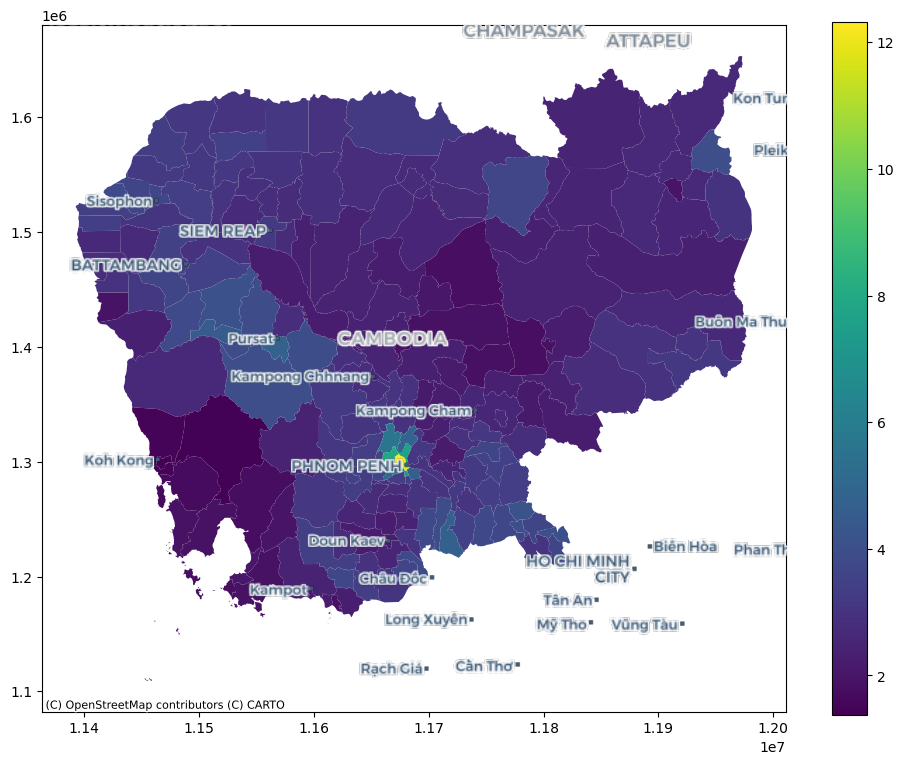
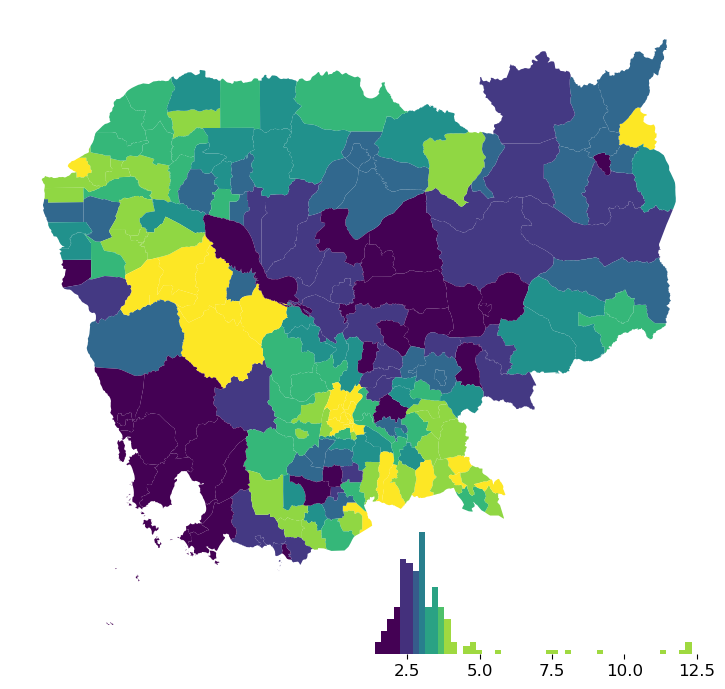
We will use the average measurement of nitrogen dioxide (no2_mean) by region throughout the block.

To make visualisation a bit easier below, we create an additional column with values rescaled:

db["no2_viz"] = db["no2_mean"] * 1e5

This way, numbers are larger and will fit more easily on legends:

db[["no2_mean", "no2_viz"]].describe()

	no2_mean	no2_viz
count	198.000000	198.000000
mean	0.000032	3.236567
std	0.000017	1.743538
min	0.000014	1.377641
25%	0.000024	2.427438
50%	0.000029	2.922031
75%	0.000034	3.390426
max	0.000123	12.323324

Choropleths

ax = db.to_crs(
    epsg=3857
).plot(
    "no2_viz", 
    legend=True,
    figsize=(12, 9)
)
contextily.add_basemap(
    ax, 
    source=contextily.providers.CartoDB.VoyagerOnlyLabels,
    zoom=7
);

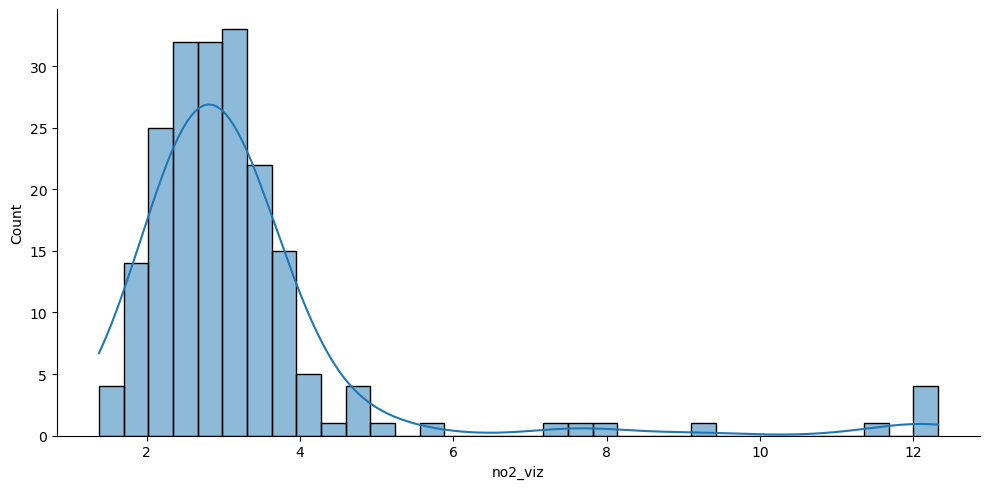
A classiffication problem

db["no2_viz"].unique().shape

(198,)

sns.displot(
    db, x="no2_viz", kde=True, aspect=2
);

How to assign colors?

Attention

To build an intuition behind each classification algorithm more easily, we create a helper method (plot_classi) that generates a visualisation of a given classification.

Toggle the cell below if you are interested in the code behind it.

def plot_classi(classi, col, db):
    """
    Illustrate a classiffication
    ...
    
    Arguments
    ---------
    classi : mapclassify.classifiers
             Classification object
    col    : str
             Column name used for `classi`
    db     : geopandas.GeoDataFrame
             Geo-table with data for
             the classification    
    """
    f, ax = plt.subplots(figsize=(12, 6))
    ax.set_title(classi.name)
    # KDE
    sns.kdeplot(
        db[col], fill=True, ax=ax
    )
    for i in range(0, len(classi.bins)-1):
        ax.axvline(classi.bins[i], color="red")
    # Map
    aux = f.add_axes([.6, .45, .32, .4])
    db.assign(lbls=classi.yb).plot(
        "lbls", cmap="viridis", ax=aux
    )
    aux.set_axis_off()
    return None

• Equal intervals

classi = mc.EqualInterval(db["no2_viz"], k=7)
classi

EqualInterval

   Interval      Count
----------------------
[ 1.38,  2.94] |   103
( 2.94,  4.50] |    80
( 4.50,  6.07] |     6
( 6.07,  7.63] |     1
( 7.63,  9.20] |     3
( 9.20, 10.76] |     0
(10.76, 12.32] |     5

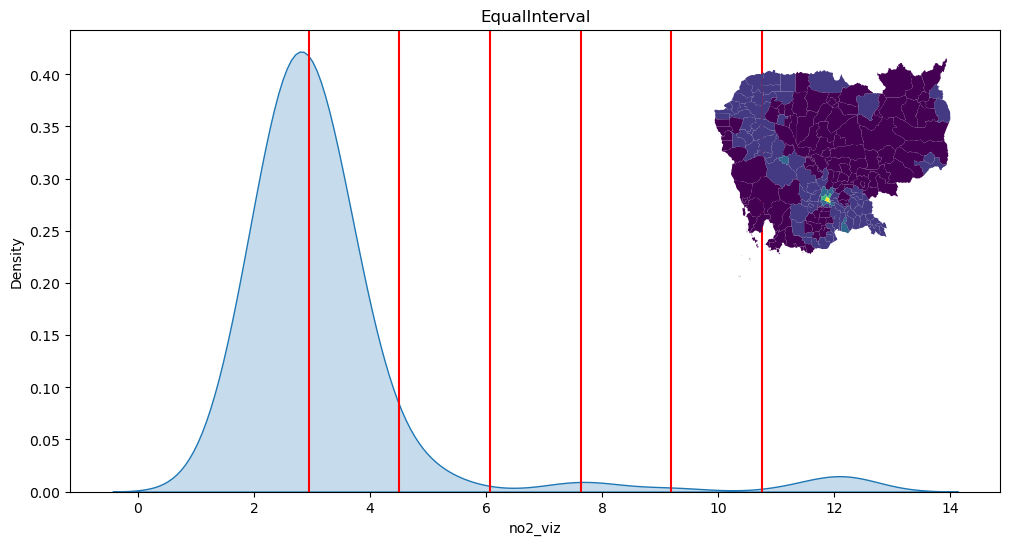
• Quantiles

classi = mc.Quantiles(db["no2_viz"], k=7)
classi

Quantiles

   Interval      Count
----------------------
[ 1.38,  2.24] |    29
( 2.24,  2.50] |    28
( 2.50,  2.76] |    28
( 2.76,  3.02] |    28
( 3.02,  3.35] |    28
( 3.35,  3.76] |    28
( 3.76, 12.32] |    29

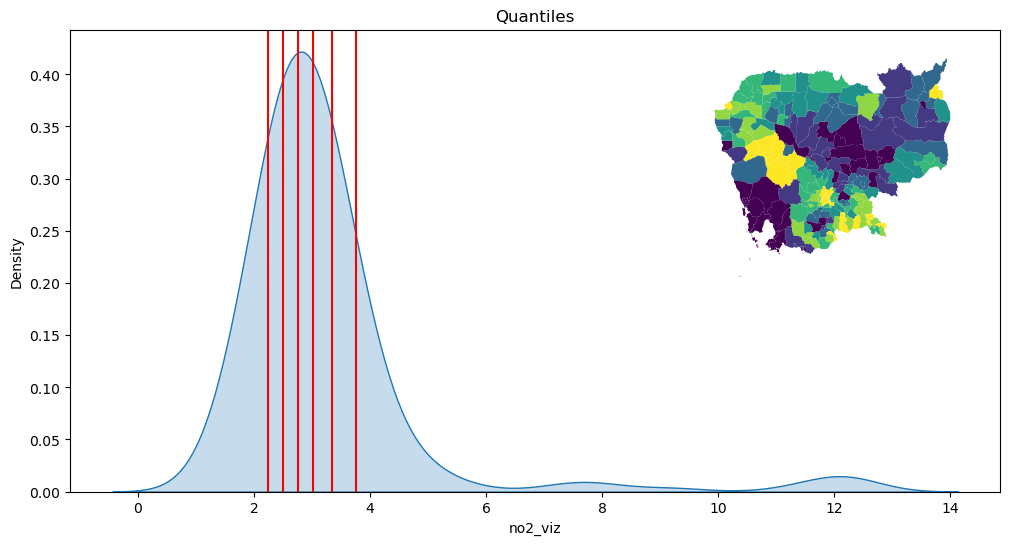
• Fisher-Jenks

classi = mc.FisherJenks(db["no2_viz"], k=7)
classi

FisherJenks

   Interval      Count
----------------------
[ 1.38,  2.06] |    20
( 2.06,  2.69] |    58
( 2.69,  3.30] |    62
( 3.30,  4.19] |    42
( 4.19,  5.64] |     7
( 5.64,  9.19] |     4
( 9.19, 12.32] |     5

---

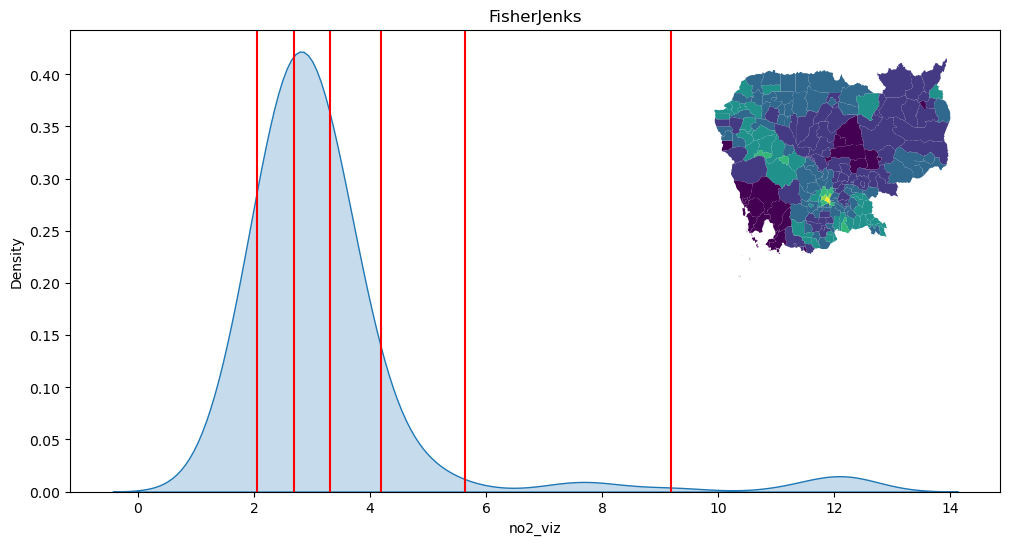
Now let’s dig into the internals of classi:

classi

FisherJenks

   Interval      Count
----------------------
[ 1.38,  2.06] |    20
( 2.06,  2.69] |    58
( 2.69,  3.30] |    62
( 3.30,  4.19] |    42
( 4.19,  5.64] |     7
( 5.64,  9.19] |     4
( 9.19, 12.32] |     5

classi.k

7

classi.bins

array([ 2.05617382,  2.6925931 ,  3.30281182,  4.19124954,  5.63804861,
        9.19190206, 12.32332434])

classi.yb

array([2, 3, 3, 1, 1, 2, 1, 1, 1, 0, 0, 3, 2, 1, 1, 1, 3, 1, 1, 1, 2, 0,
       0, 4, 2, 1, 3, 1, 0, 0, 0, 1, 2, 2, 6, 5, 4, 2, 1, 3, 2, 3, 2, 1,
       2, 3, 2, 3, 1, 1, 3, 1, 2, 3, 3, 1, 3, 3, 1, 0, 1, 1, 3, 2, 0, 0,
       2, 1, 0, 0, 0, 2, 0, 1, 3, 3, 3, 2, 3, 2, 3, 1, 2, 3, 1, 1, 1, 1,
       2, 1, 2, 2, 1, 2, 2, 2, 1, 3, 2, 3, 2, 2, 2, 1, 2, 3, 3, 2, 0, 3,
       1, 0, 1, 2, 1, 1, 2, 1, 2, 6, 5, 6, 2, 2, 3, 6, 3, 4, 3, 4, 2, 3,
       0, 2, 5, 6, 4, 5, 2, 2, 2, 1, 1, 1, 2, 1, 2, 3, 3, 2, 2, 2, 3, 2,
       1, 1, 3, 4, 2, 1, 3, 1, 2, 3, 4, 0, 1, 1, 2, 1, 2, 2, 2, 2, 1, 2,
       2, 2, 0, 0, 1, 2, 3, 3, 3, 3, 3, 2, 1, 2, 1, 1, 1, 2, 2, 1, 3, 1])

How many colors?

Attention

The code used to generate this figure uses more advanced features than planned for this course.

If you want to inspect it, toggle the cell below.

vals = [3, 5, 7, 9, 12, 15]
algos = ["equal_interval", "quantiles", "fisherjenks"]
f, axs = plt.subplots(
    len(algos), len(vals), figsize=(3*len(vals), 3*len(algos))
)
for i in range(len(algos)):
    for j in range(len(vals)):
        db.plot(
            "no2_viz", scheme=algos[i], k=vals[j], ax=axs[i, j]
        )
        axs[i, j].set_axis_off()
        if i==0:
            axs[i, j].set_title(f"k={vals[j]}")
        if j==0:
            axs[i, j].text(
                -0.1, 
                0.5, 
                algos[i], 
                horizontalalignment='center',
                verticalalignment='center', 
                transform=axs[i, j].transAxes,
                rotation=90
            )

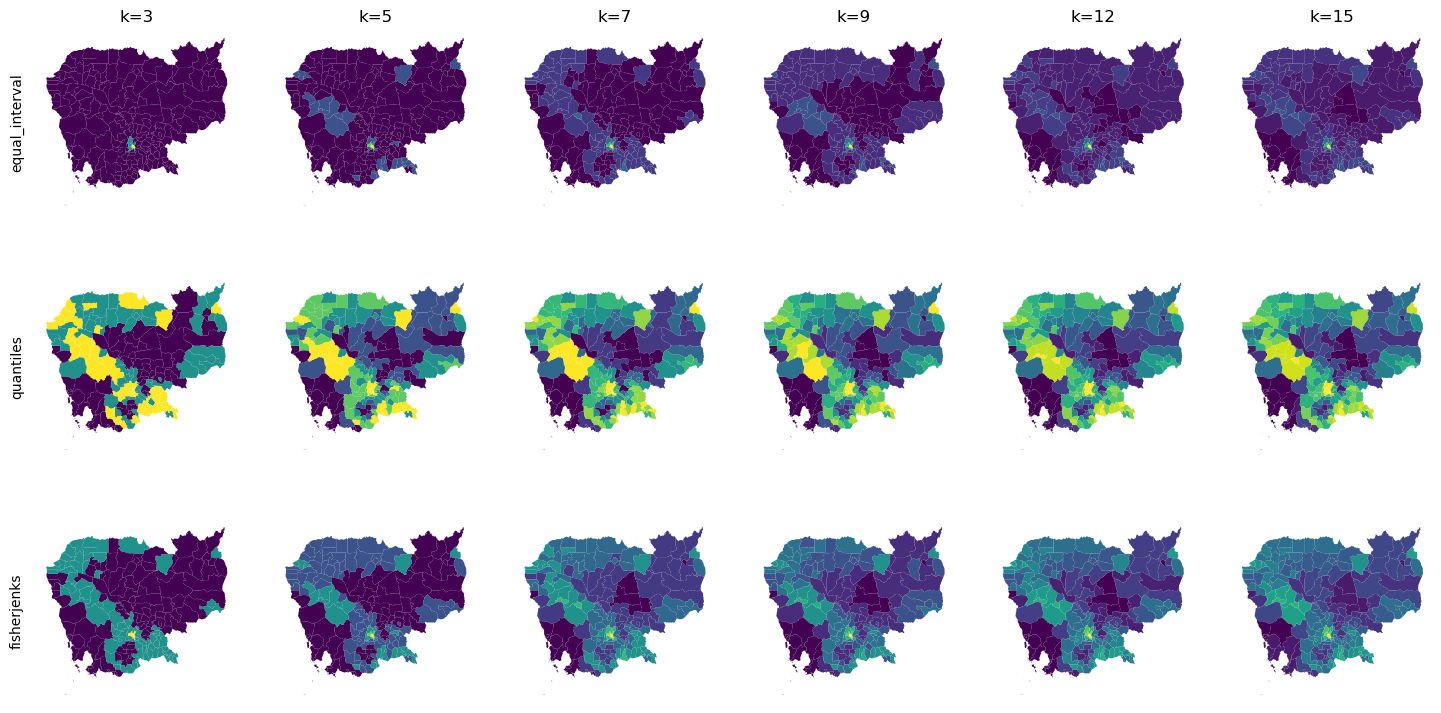
Using the right color

For a safe choice, make sure to visit ColorBrewer

• Categories, non-ordered

• Graduated, sequential

• Graduated, divergent

Choropleths on Geo-Tables

Streamlined

How can we create classifications from data on geo-tables? Two ways:

• Directly within plot (only for some algorithms)

db.plot(
    "no2_viz", scheme="quantiles", k=7, legend=True
);

See this tutorial for more details on fine tuning choropleths manually

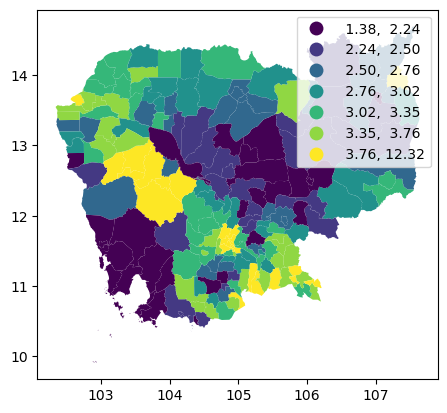
Challenge

Create an equal interval map with five bins for no2_viz

Manual approach

This is valid for any algorithm and provides much more flexibility at the cost of effort.

classi = mc.Quantiles(db["no2_viz"], k=7)
db.assign(
    classes=classi.yb
).plot("classes");

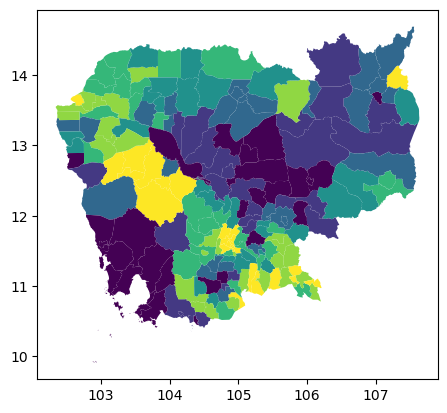
Value by alpha mapping

See here for more examples of VBA mapping.

db['area_inv'] = 1 / db.to_crs(epsg=5726).area

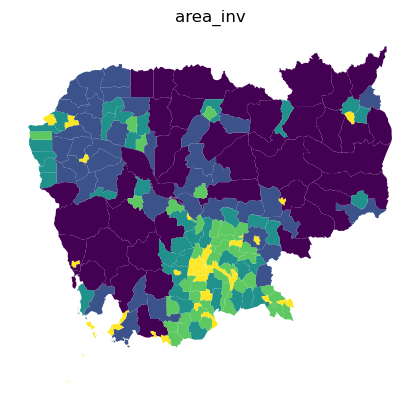
# Set up figure and axis
f, ax = plt.subplots(1, figsize=(12, 9))
# VBA choropleth
vba_choropleth(
    'no2_viz',          # Column for color 
    'area_inv',         # Column for transparency (alpha)
    db,                 # Geo-table
    rgb_mapclassify={   # Options for color classification
        'classifier': 'quantiles', 'k':5
    },
    alpha_mapclassify={ # Options for alpha classification
        'classifier': 'quantiles', 'k':5
    },
    legend=True,        # Add legend
    ax=ax               # Axis
)
# Add boundary lines
db.plot(color='none', linewidth=0.05, ax=ax);

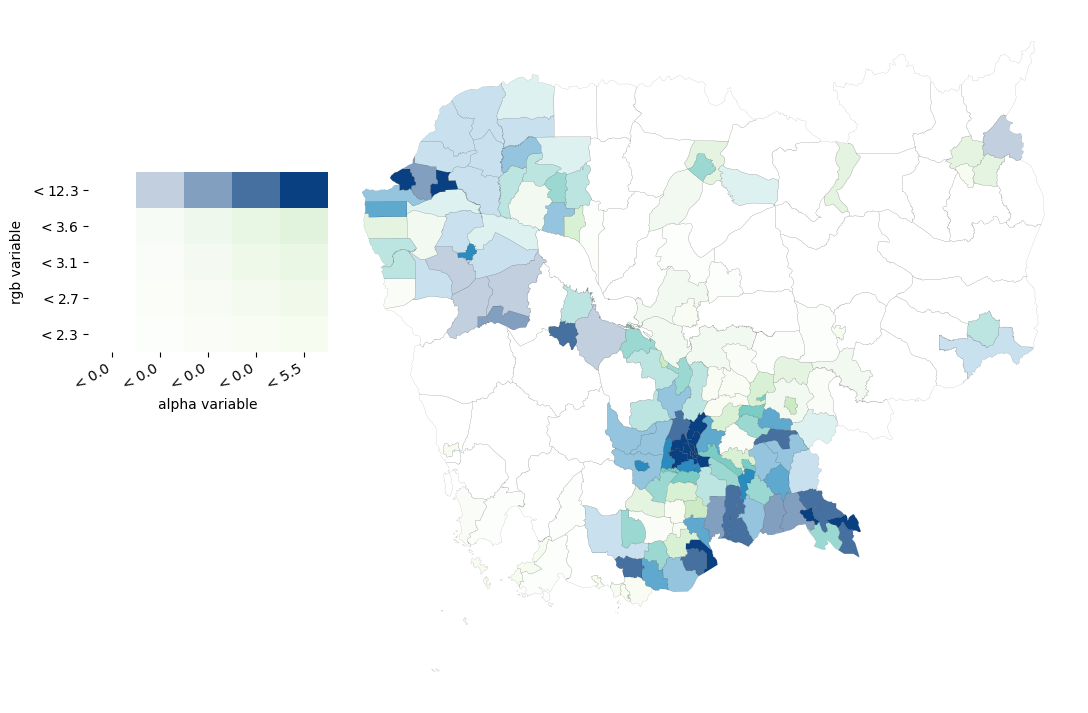
Legendgrams

Legendgrams are a way to more closely connect the statistical characteristics of your data to the map display.

Warning

Legendgrams are experimental at the moment so the code is a bit more involved and less stable. Use at your own risk!

Unfold the cell for an example.

f, ax = plt.subplots(figsize=(9, 9))

classi = mc.Quantiles(db["no2_viz"], k=7)

db.assign(
    classes=classi.yb
).plot("classes", ax=ax)

legendgram(
    f,                   # Figure object
    ax,                  # Axis object of the map
    db["no2_viz"],       # Values for the histogram
    classi.bins,         # Bin boundaries
    pal=palmpl.Viridis_7,# color palette (as palettable object)
    legend_size=(.5,.2), # legend size in fractions of the axis
    loc = 'lower right', # matplotlib-style legend locations
)
ax.set_axis_off();

Challenge

Give Task I in this block of the GDS course a go.

Choropleths on surfaces

Data

If you want to read more about the data sources behind this dataset, head to the Datasets section

Local files

Assuming you have the file locally on the path ../data/:

grid = xarray.open_rasterio(
    "../data/cambodia_s5_no2.tif"
).sel(band=1)

Online read

If you’re online, you can do:

grid = xarray.open_rasterio(
    "https://darribas.org/gds4ae/_downloads/0d14506cd792aecf73dd0f7f027e95b4/cambodia_s5_no2.tif"
).sel(band=1)

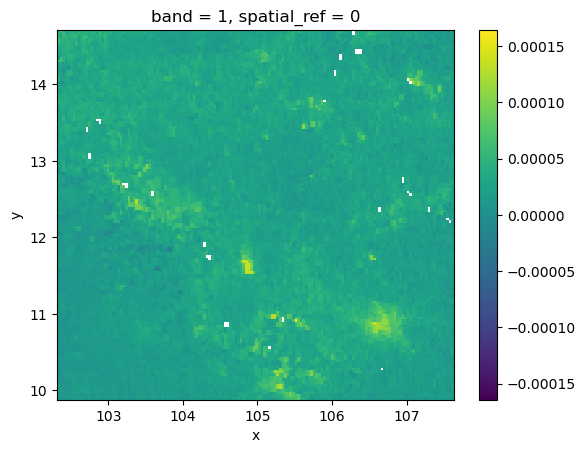
• (Implicit) continuous equal interval

grid.where(
    grid != grid.rio.nodata
).plot(cmap="viridis");

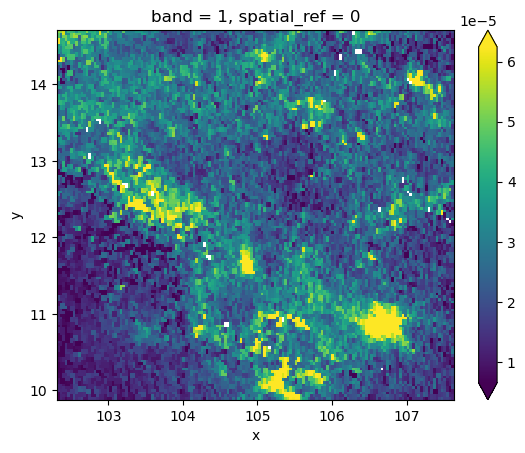
grid.where(
    grid != grid.rio.nodata
).plot(cmap="viridis", robust=True);

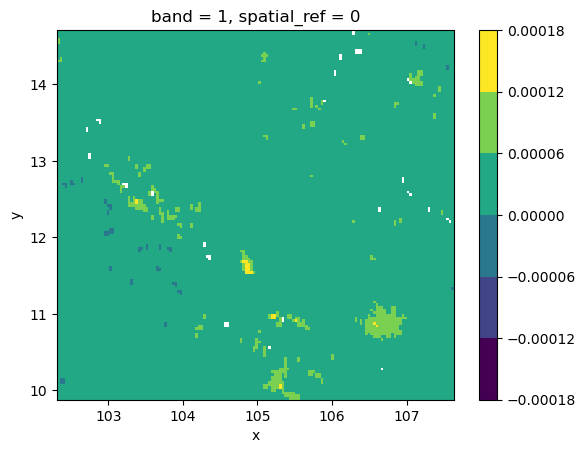
• Discrete equal interval

grid.where(
    grid != grid.rio.nodata
).plot(cmap="viridis", levels=7)

<matplotlib.collections.QuadMesh at 0x7fdd6012bcd0>

• Combining with mapclassify

grid_nona = grid.where(
    grid != grid.rio.nodata
)

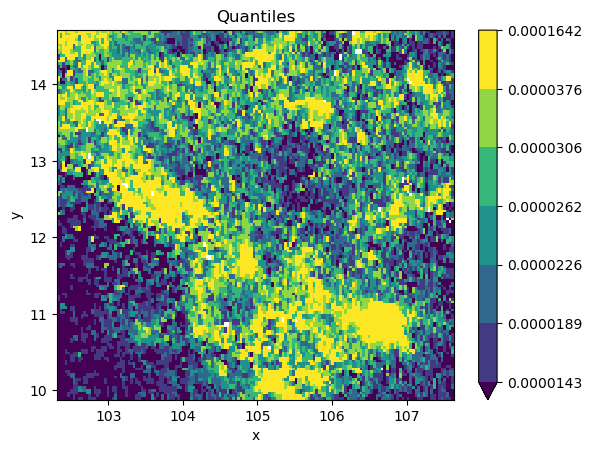
classi = mc.Quantiles(
    grid_nona.to_series().dropna(), k=7
)

grid_nona.plot(
    cmap="viridis", levels=classi.bins
)
plt.title(classi.name);

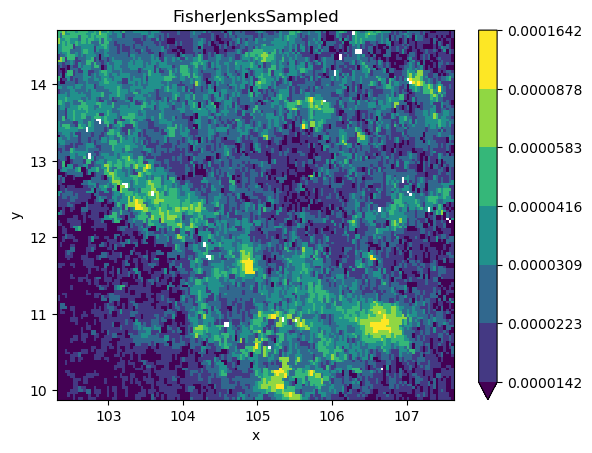
grid_nona = grid.where(
    grid != grid.rio.nodata
)

classi = mc.FisherJenksSampled(
    grid_nona.to_series().dropna().values, k=7
)

grid_nona.plot(
    cmap="viridis", levels=classi.bins
)
plt.title(classi.name);

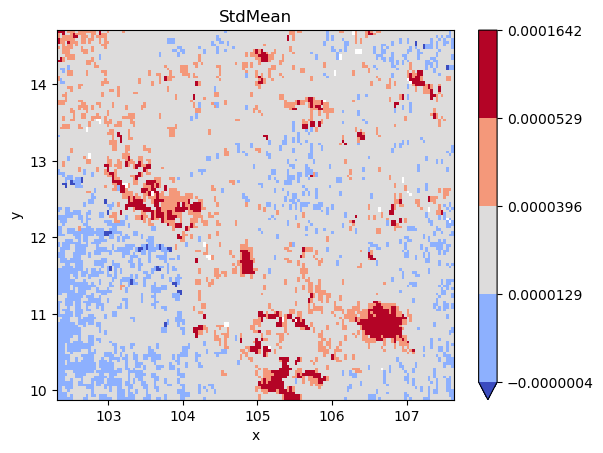
grid_nona = grid.where(
    grid != grid.rio.nodata
)

classi = mc.StdMean(
    grid_nona.to_series().dropna().values
)

grid_nona.plot(
    cmap="coolwarm", levels=classi.bins
)
plt.title(classi.name);

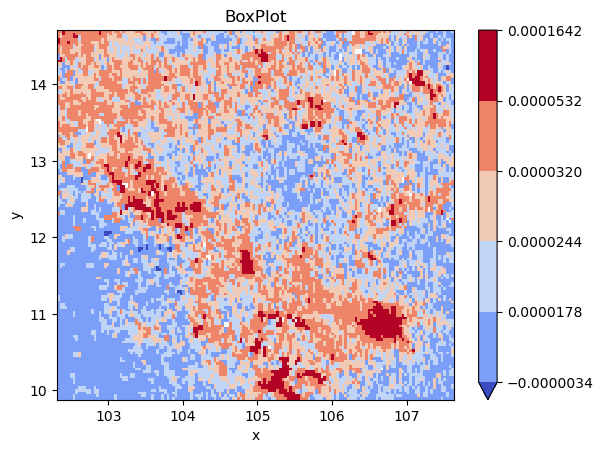
grid_nona = grid.where(
    grid != grid.rio.nodata
)

classi = mc.BoxPlot(
    grid_nona.to_series().dropna().values
)

grid_nona.plot(
    cmap="coolwarm", levels=classi.bins
)
plt.title(classi.name);

Challenge

Read the satellite image for Madrid used in the previous section and create three choropleths, one for each band, using the colormaps Reds, Greens, Blues.

Play with different classification algorithms.

• Do the results change notably?

• If so, why do you think that is?

🐾 Next steps

If you are interested in statistical maps based on classification, here are two recommendations to check out next:

• On the technical side, the documentation for mapclassify (including its tutorials) provides more detail and illustrates more classification algorithms than those reviewed in this block

• On a more conceptual note, Cynthia Brewer’s “Designing better maps” [Bre15] is an excellent blueprint for good map making.

previous

Spatial Data

next

Spatial Feature Engineering (I)