Contents

Inference

👨‍🏫 [Sync]

%matplotlib inline
from IPython.display import Image

import pandas
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
from sklearn.preprocessing import scale
from sklearn import metrics

Assuming you have the file downloaded on the path ../data/:

db = pandas.read_csv("../data/paris_abb.csv.zip")

If you’re online, you can do:

db = pandas.read_csv("https://github.com/darribas/data_science_studio/raw/master/content/data/paris_abb.csv.zip")

db['l_price'] = np.log1p(db['Price'])
db.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 50280 entries, 0 to 50279
Data columns (total 11 columns):
 #   Column                  Non-Null Count  Dtype  
---  ------                  --------------  -----  
 0   id                      50280 non-null  int64  
 1   neighbourhood_cleansed  50280 non-null  object 
 2   property_type           50280 non-null  object 
 3   room_type               50280 non-null  object 
 4   accommodates            50280 non-null  int64  
 5   bathrooms               50280 non-null  float64
 6   bedrooms                50280 non-null  float64
 7   beds                    50280 non-null  float64
 8   bed_type                50280 non-null  object 
 9   Price                   50280 non-null  float64
 10  l_price                 50280 non-null  float64
dtypes: float64(5), int64(2), object(4)
memory usage: 4.2+ MB

Baseline model

\[ \log(P) = \alpha + X \beta + \epsilon \]

\(X\):

  • Bathrooms

  • Bedrooms

  • Beds

  • Room type

m1 = sm.ols('l_price ~ bedrooms + bathrooms + beds', db).fit()
m1.summary()
OLS Regression Results
Dep. Variable: l_price R-squared: 0.245
Model: OLS Adj. R-squared: 0.245
Method: Least Squares F-statistic: 5433.
Date: Thu, 07 Jan 2021 Prob (F-statistic): 0.00
Time: 17:25:24 Log-Likelihood: -38592.
No. Observations: 50280 AIC: 7.719e+04
Df Residuals: 50276 BIC: 7.723e+04
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 4.1806 0.005 852.126 0.000 4.171 4.190
bedrooms 0.2253 0.004 57.760 0.000 0.218 0.233
bathrooms -0.1544 0.005 -32.373 0.000 -0.164 -0.145
beds 0.1398 0.003 50.554 0.000 0.134 0.145
Omnibus: 11384.882 Durbin-Watson: 1.846
Prob(Omnibus): 0.000 Jarque-Bera (JB): 585415.122
Skew: -0.096 Prob(JB): 0.00
Kurtosis: 19.715 Cond. No. 7.94


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

To note:

  • Decent \(R^2\) (although that’s not holy truth)

  • Every variable significant and related as expected

  • Interpret coefficients

cols = ['bedrooms', 'bathrooms', 'beds']
scX = pandas.DataFrame(scale(db[cols]),
                       index=db.index,
                       columns=cols)
scX.describe()
bedrooms bathrooms beds
count 5.028000e+04 5.028000e+04 5.028000e+04
mean 1.748138e-14 1.621070e-15 -5.895298e-15
std 1.000010e+00 1.000010e+00 1.000010e+00
min -1.076738e+00 -1.625116e+00 -1.429042e+00
25% -7.772733e-02 -1.702805e-01 -5.706025e-01
50% -7.772733e-02 -1.702805e-01 -5.706025e-01
75% -7.772733e-02 -1.702805e-01 2.878366e-01
max 4.887380e+01 7.111664e+01 4.149292e+01 
m2 = sm.ols('l_price ~ bedrooms + bathrooms + beds', 
            data=scX.join(db['l_price']))\
       .fit()
m2.summary()
OLS Regression Results
Dep. Variable: l_price R-squared: 0.245
Model: OLS Adj. R-squared: 0.245
Method: Least Squares F-statistic: 5433.
Date: Thu, 07 Jan 2021 Prob (F-statistic): 0.00
Time: 17:25:24 Log-Likelihood: -38592.
No. Observations: 50280 AIC: 7.719e+04
Df Residuals: 50276 BIC: 7.723e+04
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 4.4837 0.002 1928.462 0.000 4.479 4.488
bedrooms 0.2255 0.004 57.760 0.000 0.218 0.233
bathrooms -0.1061 0.003 -32.373 0.000 -0.113 -0.100
beds 0.1628 0.003 50.554 0.000 0.156 0.169
Omnibus: 11384.882 Durbin-Watson: 1.846
Prob(Omnibus): 0.000 Jarque-Bera (JB): 585415.122
Skew: -0.096 Prob(JB): 0.00
Kurtosis: 19.715 Cond. No. 3.11


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Let’s bring both sets of results together:

pandas.DataFrame({"Baseline": m1.params,
                  "X Std.": m2.params
                 })
Baseline X Std.
Intercept 4.180599 4.483657
bedrooms 0.225325 0.225548
bathrooms -0.154385 -0.106119
beds 0.139759 0.162806

To note:

How does interpretation of the coefficients change?

  • Meaning of intecept when \(X\) is demeanded

  • Units in which \(\beta\) are interpreted

Predictive checking

Is the model picking up the overall “shape of data”?

  • Important to know how much we should trust our inferences

  • Crucial if we want to use the model to predict!

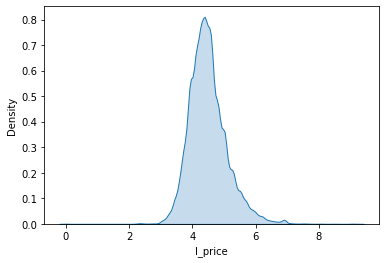
sns.kdeplot(db['l_price'], shade=True)

<AxesSubplot:xlabel='l_price', ylabel='Density'>
../../_images/08-Inference_14_1.png 
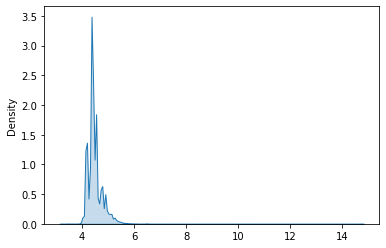
sns.kdeplot(m1.fittedvalues, shade=True)

<AxesSubplot:ylabel='Density'>
../../_images/08-Inference_15_1.png 
f, ax = plt.subplots(1, figsize=(9, 6))
sns.kdeplot(db['l_price'], shade=True, ax=ax, label='$y$')
sns.kdeplot(m1.fittedvalues, shade=True, ax=ax, label='$\hat{y}$')
plt.show()
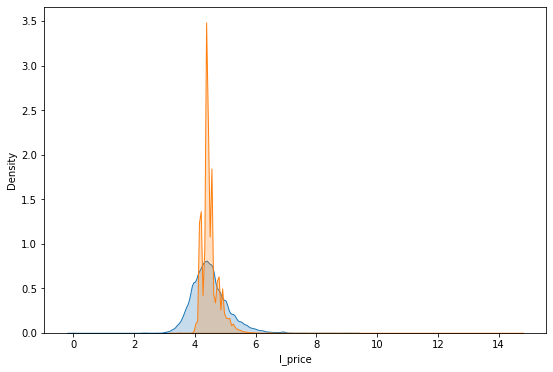
../../_images/08-Inference_16_0.png

To note:

  • Not a terrible start

  • How could we improve it?

m3 = sm.ols('l_price ~ bedrooms + bathrooms + beds + room_type', db).fit()
m3.summary()
OLS Regression Results
Dep. Variable: l_price R-squared: 0.340
Model: OLS Adj. R-squared: 0.340
Method: Least Squares F-statistic: 4314.
Date: Thu, 07 Jan 2021 Prob (F-statistic): 0.00
Time: 17:25:25 Log-Likelihood: -35210.
No. Observations: 50280 AIC: 7.043e+04
Df Residuals: 50273 BIC: 7.050e+04
Df Model: 6
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 4.2417 0.005 899.941 0.000 4.232 4.251
room_type[T.Hotel room] 0.5548 0.016 35.619 0.000 0.524 0.585
room_type[T.Private room] -0.4862 0.007 -66.604 0.000 -0.501 -0.472
room_type[T.Shared room] -1.0320 0.028 -36.320 0.000 -1.088 -0.976
bedrooms 0.2388 0.004 65.134 0.000 0.232 0.246
bathrooms -0.1440 0.004 -32.285 0.000 -0.153 -0.135
beds 0.1144 0.003 43.386 0.000 0.109 0.120
Omnibus: 11695.728 Durbin-Watson: 1.878
Prob(Omnibus): 0.000 Jarque-Bera (JB): 680804.847
Skew: -0.027 Prob(JB): 0.00
Kurtosis: 21.027 Cond. No. 37.2


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
f, ax = plt.subplots(1, figsize=(9, 6))
sns.kdeplot(db['l_price'], shade=True, ax=ax, label='$y$')
sns.kdeplot(m1.fittedvalues, shade=True, ax=ax, label='$\hat{y}_1$')
sns.kdeplot(m3.fittedvalues, shade=True, ax=ax, label='$\hat{y}_2$')
plt.show()
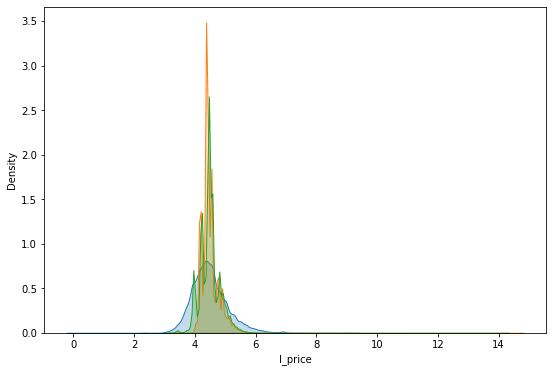
../../_images/08-Inference_19_0.png

To note:

  • This is better!

  • But these are only point predictions. Sometimes that’s good enough.

  • Usually however, we want a model to capture the underlying process instead of the particular realisation observed (ie. dataset).

  • Then we need to think about the uncertainty embedded in the model we are estimating

Inferential Vs Predictive uncertainty

[See more in Chapter 7.2 of Gelman & Hill 2006 👌💯]

  • Two types of uncertainty in our model

    • Predictive (\(\epsilon\))

    • Inferential (\(\beta\))

  • Both affect the final predictions we make

Image("../figs/abb_room.png", retina=True)
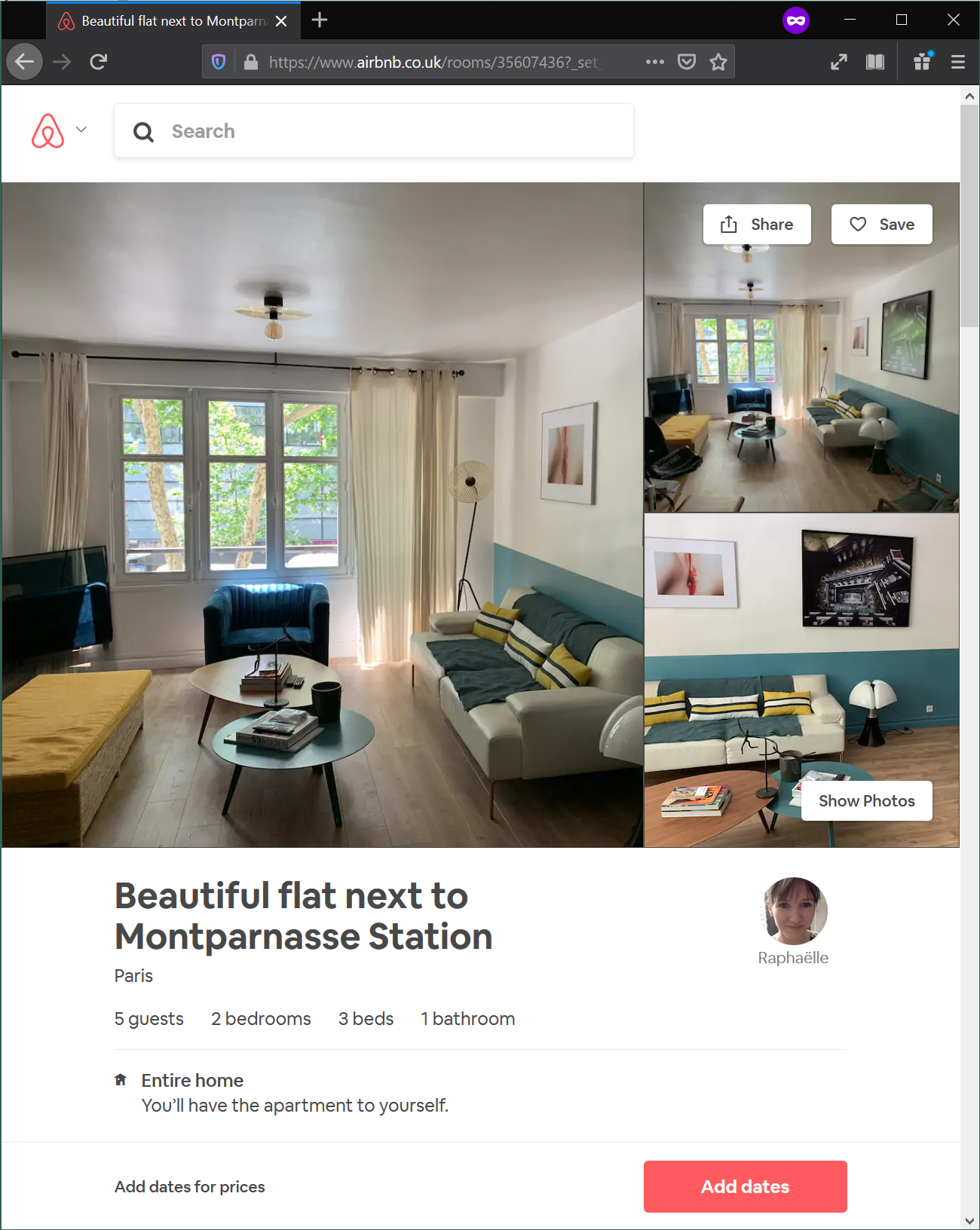
../../_images/08-Inference_22_0.png 
room = db.loc[db['id']==35607436, :]
room.T
45979
id 35607436
neighbourhood_cleansed Luxembourg
property_type Apartment
room_type Entire home/apt
accommodates 5
bathrooms 1
bedrooms 2
beds 3
bed_type Real Bed
Price 90
l_price 4.51086 
rid = room.index[0]
db.loc[rid, :]

id                               35607436
neighbourhood_cleansed         Luxembourg
property_type                   Apartment
room_type                 Entire home/apt
accommodates                            5
bathrooms                               1
bedrooms                                2
beds                                    3
bed_type                         Real Bed
Price                                  90
l_price                           4.51086
Name: 45979, dtype: object
\[ \hat{\log(P_i)} = \alpha + \sum_k \beta_k * X_k \]
m1.params['Intercept'] + db.loc[rid, cols].dot(m1.params[cols])

4.896141184855212

To note:

  • What does dot do?

m1.fittedvalues[rid]

4.896141184855212

Point predictive simulation

%%time
# Parameters
## Number of simulations
r = 2000
# Pull out characteristics for house of interest
x_i = db.loc[rid, cols]
# Specify model engine
model = m1

# Place-holder
sims = np.zeros(r)
# Loop over number of replications
for i in range(r):
    # Get a random draw of betas
    rbs = np.random.normal(model.params, model.bse)
    # Get a random draw of epsilon
    re = np.random.normal(0, model.scale)
    # Obtain point estimate
    y_hr = rbs[0] + np.dot(x_i, rbs[1:]) + re
    # Store estimate
    sims[i] = y_hr

CPU times: user 637 ms, sys: 35.1 ms, total: 672 ms
Wall time: 632 ms

f, ax = plt.subplots(1, figsize=(12, 6))

sns.kdeplot(sims, shade=True, ax=ax, label='Simulation')
ax.axvline(db.loc[rid, 'l_price'], c='orange', label='Observed')
ax.axvline(model.fittedvalues[rid], c='green', label='Predicted')

lo, up = pandas.Series(sims)\
               .sort_values()\
               .iloc[[int(np.round(0.025 * r)), int(np.round(0.975 * r))]]
ax.axvline(lo, c='grey', linewidth=1)
ax.axvline(up, c='grey', linewidth=1)

plt.legend()
plt.show()
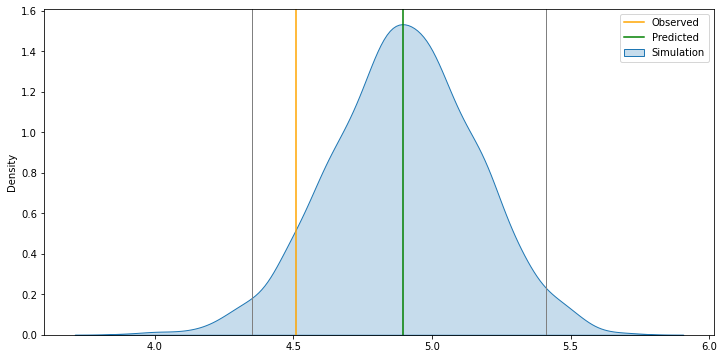
../../_images/08-Inference_31_0.png

To note:

  • Intuition of the simulation

  • The for loop, deconstructed

  • The graph, bit by bit

  • If we did this for every observation, we’d expect 95% to be within the 95% bands

Exercise

Explore with the code above and try to generate similar plots for:

  • Different houses across locations and characteristics

  • Different model

Exercise+

Recreate the analysis above for observation 5389821. What happens? Why?

Now, we could do this for all the observations and get a sense of the overall distribution to be expected

%%time
# Parameters
## Number of observations & simulations
n = db.shape[0]
r = 200
# Specify model engine
model = m1

# Place-holder (N, r)
sims = np.zeros((n, r))
# Loop over number of replications
for i in range(r):
    # Get a random draw of betas
    rbs = np.random.normal(model.params, model.bse)
    # Get a random draw of epsilon
    re = np.random.normal([0]*n, model.scale)
    # Obtain point estimate
    y_hr = rbs[0] + np.dot(db[cols], rbs[1:]) + re
    # Store estimate
    sims[:, i] = y_hr

CPU times: user 5.61 s, sys: 27.3 s, total: 32.9 s
Wall time: 2.08 s

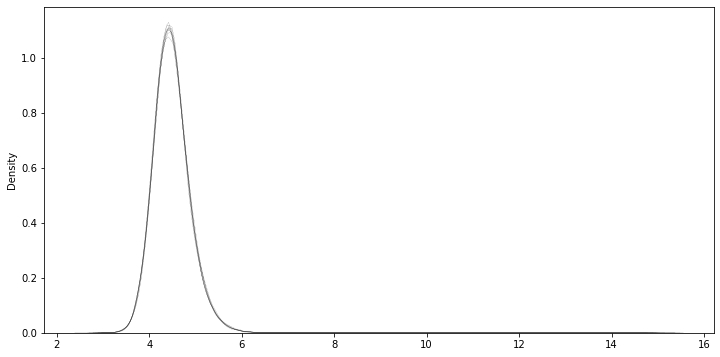
f, ax = plt.subplots(1, figsize=(12, 6))

for i in range(10):
    sns.kdeplot(sims[:, i], ax=ax, linewidth=0.1, alpha=0.1, color='k')
    
plt.show()
../../_images/08-Inference_34_0.png 
f, ax = plt.subplots(1, figsize=(12, 6))

sns.kdeplot(db['l_price'], shade=True, ax=ax, label='$y$')
sns.kdeplot(m1.fittedvalues, shade=True, ax=ax, label='$\hat{y}$')

for i in range(r):
    sns.kdeplot(sims[:, i], ax=ax, linewidth=0.1, alpha=0.1, color='k')
    
plt.show()
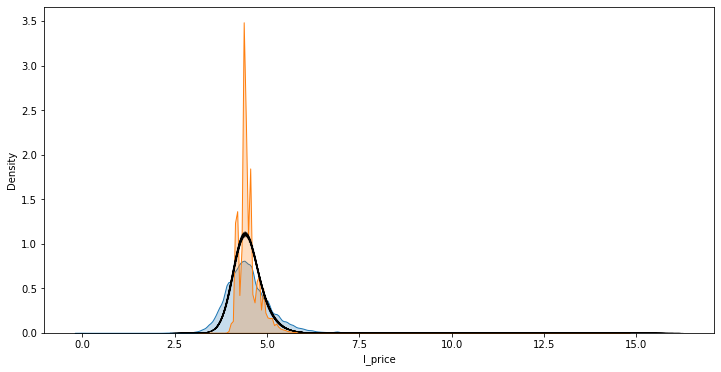
../../_images/08-Inference_35_0.png

To note:

  • Black line contains r thin lines that collectively capture the uncertainty behind the model

New data

Imagine we are trying to figure out how much should we charge for a property we want to put on AirBnb.

For example, let’s assume our property is:

new = pandas.Series({'bedrooms': 4,
                     'bathrooms': 1,
                     'beds': 8})

%%time
# Parameters
## Number of simulations
r = 2000
# Pull out characteristics for house of interest
x_i = new
# Specify model engine
model = m1

# Place-holder
sims = np.zeros(r)
# Loop over number of replications
for i in range(r):
    # Get a random draw of betas
    rbs = np.random.normal(model.params, model.bse)
    # Get a random draw of epsilon
    re = np.random.normal(0, model.scale)
    # Obtain point estimate
    y_hr = rbs[0] + np.dot(x_i, rbs[1:]) + re
    # Store estimate
    sims[i] = y_hr

CPU times: user 640 ms, sys: 4.53 ms, total: 644 ms
Wall time: 643 ms

f, ax = plt.subplots(1, figsize=(12, 6))

sns.kdeplot(sims, shade=True, ax=ax, label='Simulation')
ax.axvline(model.params.iloc[0] + np.dot(new, model.params.iloc[1:]), \
           c='green', label='Predicted')

lo, up = pandas.Series(sims)\
               .sort_values()\
               .iloc[[int(np.round(0.025 * r)), int(np.round(0.975 * r))]]
ax.axvline(lo, c='grey', linewidth=1)
ax.axvline(up, c='grey', linewidth=1)

plt.legend()
plt.show()
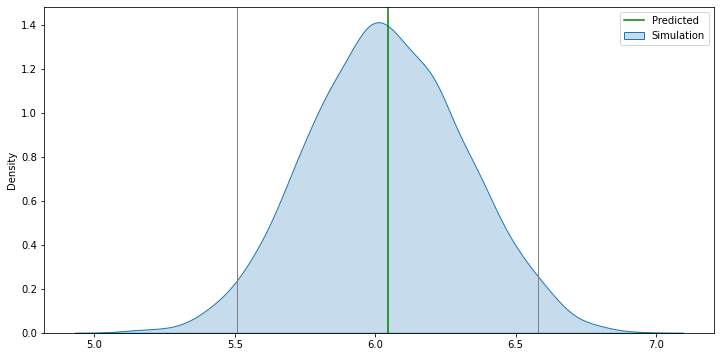
../../_images/08-Inference_40_0.png

[Pro]

def predictor(bedrooms, bathrooms, beds):
    new = pandas.Series({'bedrooms': bedrooms,
                         'bathrooms': bathrooms,
                         'beds': beds
                        })
    r = 1000
    x_i = new
    model = m1
    y_hat = model.params.iloc[0] + np.dot(new, model.params.iloc[1:])
    # Simulation
    sims = np.zeros(r)
    for i in range(r):
        rbs = np.random.normal(model.params, model.bse)
        re = np.random.normal(0, model.scale)
        y_hr = rbs[0] + np.dot(x_i, rbs[1:]) + re
        sims[i] = y_hr
    sims = np.exp(sims)
    y_hat = np.exp(y_hat)    
    # Bands
    lo, up = pandas.Series(sims)\
                   .sort_values()\
                   .iloc[[int(np.round(0.025 * r)), int(np.round(0.975 * r))]]
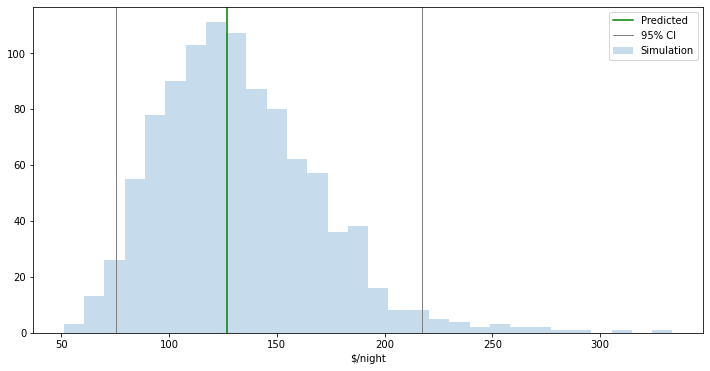
    # Setup'n'draw figure
    f, ax = plt.subplots(1, figsize=(12, 6))
    ax.hist(sims, label='Simulation', alpha=0.25, bins=30)
    ax.axvline(y_hat, c='green', label='Predicted')
    ax.axvline(lo, c='grey', linewidth=1, label='95% CI')
    ax.axvline(up, c='grey', linewidth=1)
    #ax.set_xlim((0, 10))
    # Dress up
    ax.set_xlabel("$/night")
    plt.legend()
    return plt.show()

predictor(3, 1, 1)
../../_images/08-Inference_42_0.png 
# You might have to run this to make interactives work
# jupyter labextension install @jupyter-widgets/jupyterlab-manager
# From https://ipywidgets.readthedocs.io/en/latest/user_install.html#installing-the-jupyterlab-extension
# Then restart Jupyter Lab
from ipywidgets import interact, IntSlider

interact(predictor, 
         bedrooms=IntSlider(min=1, max=10), \
         bathrooms=IntSlider(min=0, max=10), \
         beds=IntSlider(min=1, max=20)
        );

Model performance

To note:

  • Switch from inference to prediction

  • Overall idea of summarising model performance

  • \(R^2\)

  • Error-based measures

# R^2
r2 = pandas.Series({'Baseline': metrics.r2_score(db['l_price'],
                                                 m1.fittedvalues),
                    'Augmented': metrics.r2_score(db['l_price'],
                                                  m3.fittedvalues)})
r2

Baseline     0.244826
Augmented    0.339876
dtype: float64

# MSE
mse = pandas.Series({'Baseline': metrics.mean_squared_error(db['l_price'],
                                                            m1.fittedvalues),
                     'Augmented': metrics.mean_squared_error(db['l_price'],
                                                             m3.fittedvalues)})
mse

Baseline     0.271771
Augmented    0.237565
dtype: float64

# MAE
mae = pandas.Series({'Baseline': metrics.mean_absolute_error(db['l_price'],
                                                             m1.fittedvalues),
                     'Augmented': metrics.mean_absolute_error(db['l_price'],
                                                              m3.fittedvalues)})
mae

Baseline     0.379119
Augmented    0.357287
dtype: float64

# All
perf = pandas.DataFrame({'MAE': mae,
                         'MSE': mse,
                         'R^2': r2})
perf
MAE MSE R^2
Baseline 0.379119 0.271771 0.244826
Augmented 0.357287 0.237565 0.339876
Supervised Learning Overfitting & Cross-Validation