Geographic Data Science - Lecture VIII

Points

Dani Arribas-Bel

Today

  • The point of points
  • Point patterns
  • Visualization of point patterns

The point of points

Points like polygons

Points can represent "fixed" entities

In this case, points are qualitatively similar to polygons/lines

The goal here is, taking location fixed, to model other aspects of the data

Points like polygons

Examples:

  • Cities (in most cases)
  • Buildings
  • Polygons represented as their centroid
  • ...

When points are not polygons

Point data are not only a different geometry than polygons or lines...

... Points can also represent a fundamentally different way to approach spatial analysis

Points unlike polygons

  • Rather than exhausting the entire space, points can be events subject to occur anywhere
  • The location of the event is part of what we are trying to understand/model
  • The interest focuses on characterizing the pattern that the points follow over space

A few examples...

[Source]

[Source]

UFO Sightings (1933-)

Geo-tagged tweets

Point patterns

Point patterns

Distribution of points over a portion of space

Assumption is a point can happen anywhere on that space, but only happens in specific locations

  • Unmarked: locations only
  • Marked: values attached to each point

Point Pattern Analysis

Describe, characterize, and explain point patterns, focusing on their generating process

  • Visual exploration
  • Clustering properties and clusters
  • Statistical modeling of the underlying processes

Visualization of PPs

Visualization of PPs

Two routes (today):

  • Aggregate  ↔  "Histogram"
  • Smooth  ↔  KDE

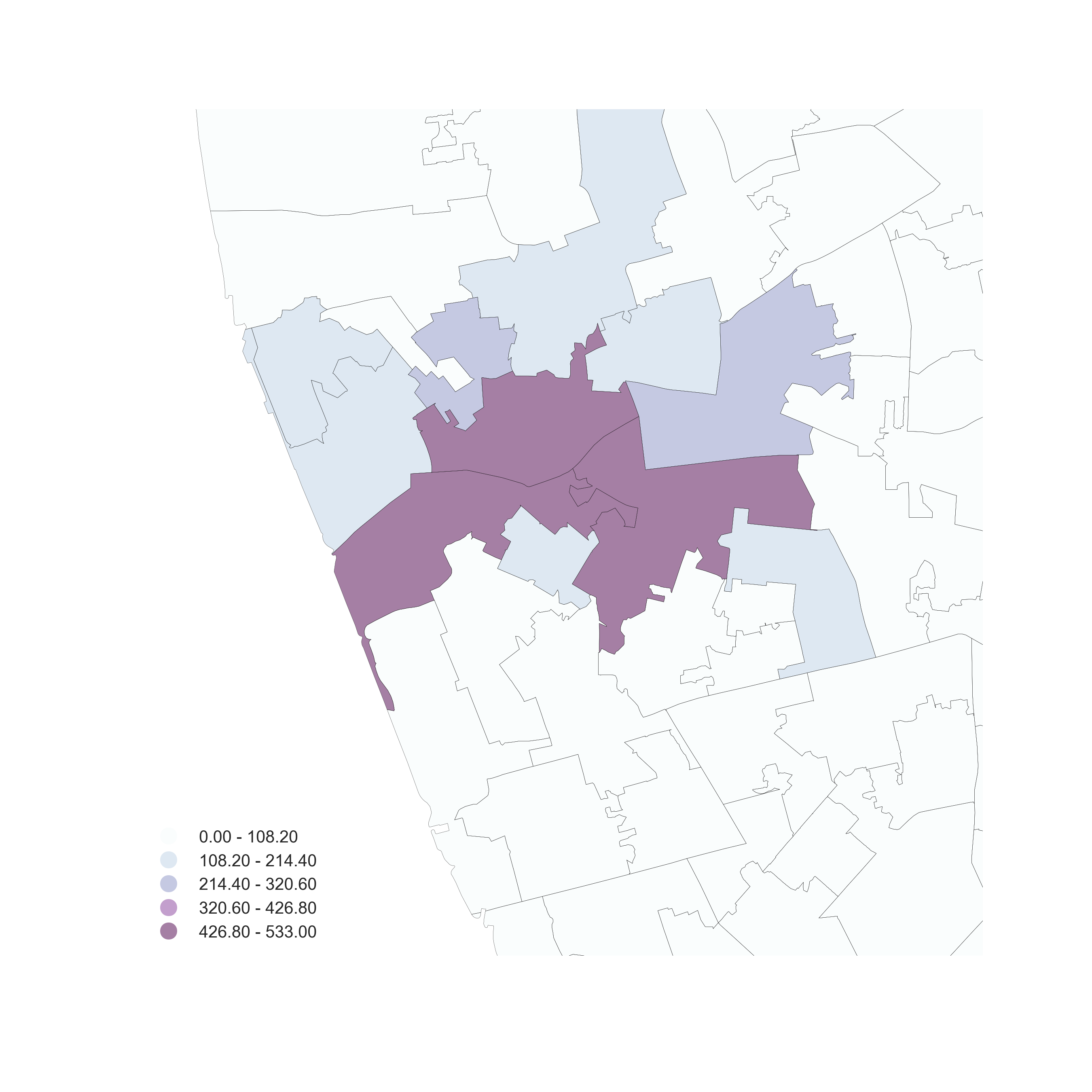
Aggregation

Points meet polygons

Use polygon boundaries and count points per area

[Insert your skills for choropleth mapping here!!!]

But, the polygons need to "make sense" (their delineation needs to relate to the point generating process)

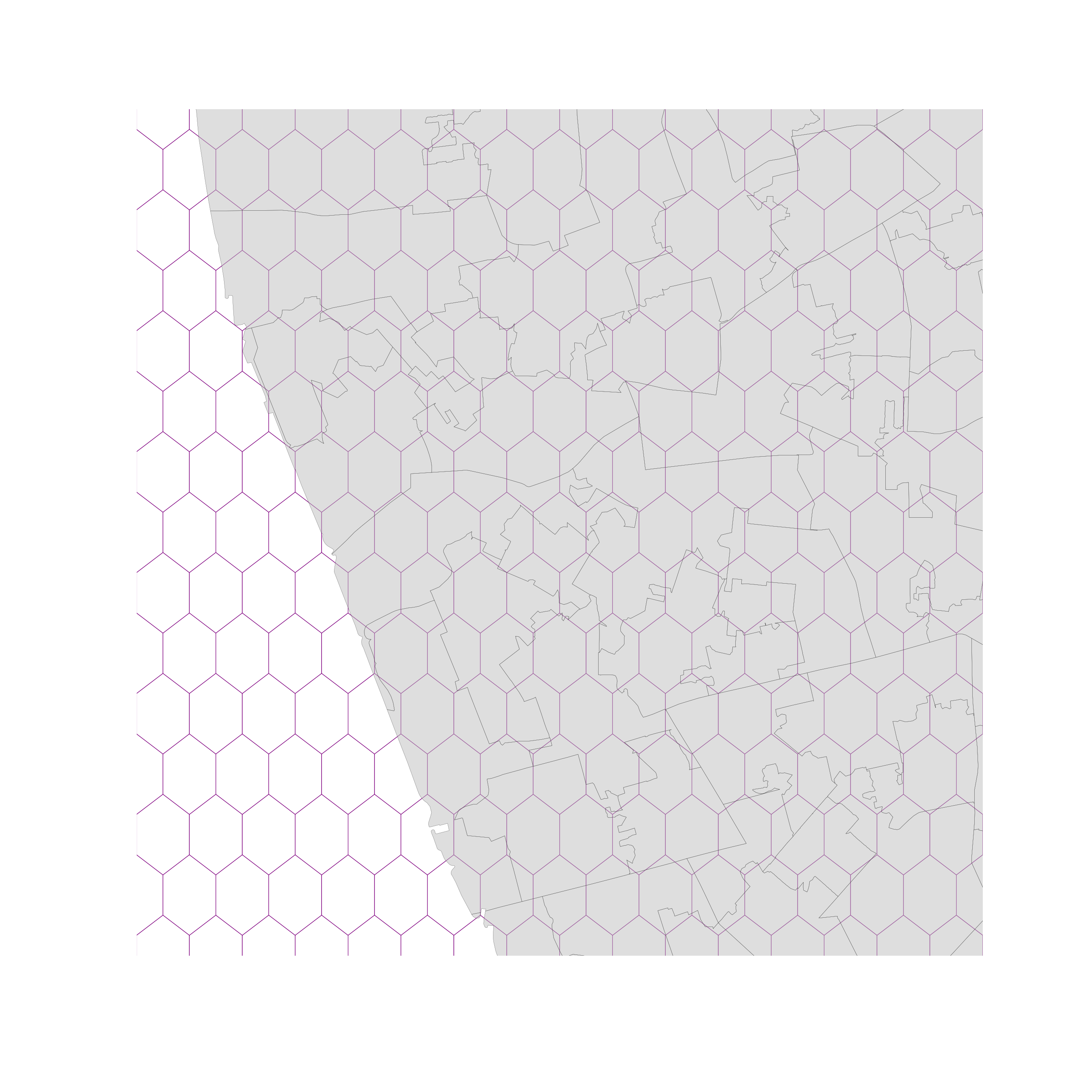
Hex-binning

If no polygon boundary seems like a good candidate for aggregation...

...draw a hexagonal (or squared) tesselation!!!

Hexagons...

  • Are regular
  • Exhaust the space (Unlike circles)
  • Have many sides (minimize boundary problems)

But...

(Arbitrary) aggregation may induce MAUP (see Lecture 4)

 + 

Points usually represent events that affect only part of the population and hence are best considered as rates (see Lecture 4)

Kernel Density Estimation

Kernel Density Estimation

Estimate the (continuous) observed distribution of a variable

  • Probability of finding an observation at a given point
  • "Continuous histogram"
  • Solves (much of) the MAUP problem, but not the underlying population issue

[Source]

Bivariate (spatial) KDE

Probability of finding observations at a given point in space

  • Bivariate version: distribution of pairs of values
  • In space: values are coordinates (XY), locations
  • Continuous "version" of a choropleth

Finding clusters of PPs

Cluster is a hard to define term

Concentrations/agglomerations of points over space, significantly more so than in the rest of the space considered

Huge literature spanning spatial analysis, statistics and computer science. Today, we'll look at...

Density

Based

Spatial

Clustering of

Applications with

Noise

DBSCAN

(Additional) Pros:

  • Not necessarily spatial
  • Very fast to run so  →  scales relatively well  →  applicable to large datasets

(Additional) Cons:

  • Not based on any probabilistic model (no inference)
  • Hard to learn about the underlying process

Creative Commons License
Geographic Data Science'16 - Lecture 8 by Dani Arribas-Bel is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.