Today

• The need to represent space formally
• Spatial weights matrices
  • What
  • Why
  • Types
• The spatial lag
• The Moran Plot

Space, formally

For a statistical method to be explicitly spatial, it needs to contain some representation of the geography, or spatial context

One of the most common ways is through Spatial Weights Matrices

• (Geo)Visualization: translating numbers into a (visual) language that the human brain "speaks better"
• Spatial Weights Matrices: translating geography into a (numerical) language that a computer "speaks better".

Core element in several spatial analysis techniques:

• Spatial autocorrelation
• Spatial clustering / geodemographics
• Spatial regression

W as a formal representation of space

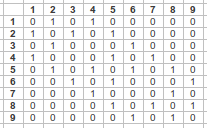
W

$$w_{ij} = \left\{ \begin{array}{rl} x > 0 &\mbox{ if $i$ and $j$ are neighbors} \\ 0 &\mbox{ otherwise} \end{array} \right\}$$ w_ii = 0 by convention

...What is a neighbor???

Types of W

A neighbor is "somebody" who is:

• Next door  →  Contiguity-based Ws
• Close  →  Distance-based Ws
• In the same "place" as us  →  Block weights
• ...

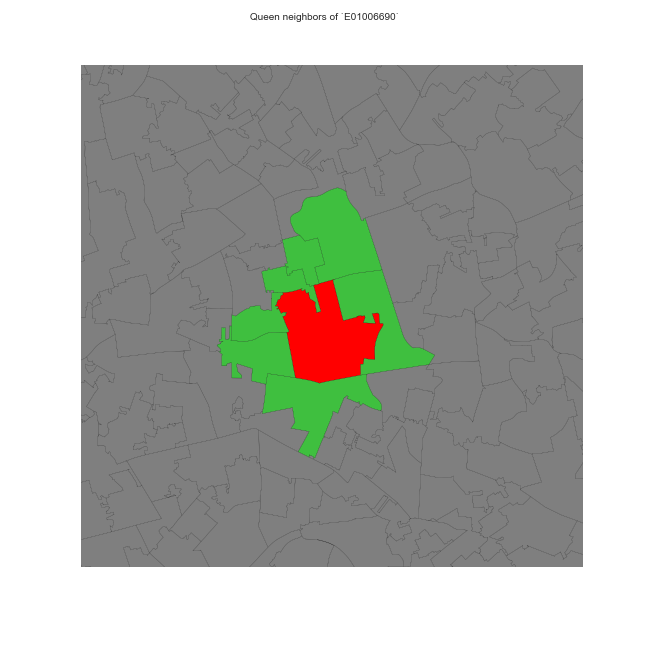
Contiguity-based weights

Sharing boundaries to any extent

• Rook
• Queen
• ...

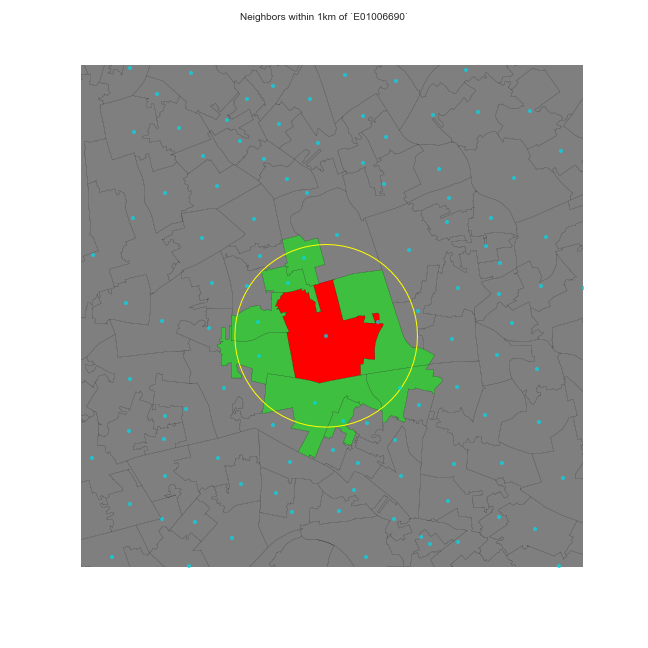
Distance-based weights

Weight is (inversely) proportional to distance between observations

• Inverse distance (threshold)
• KNN (fixed number of neighbors)
• ...

Block weights

Weights are assigned based on discretionary rules loosely related to geography

For example:

• LSOAs into MSOAs
• Post-codes within city boundaries
• Counties within states
• ...

Other types of weights

• Combinations of the above
• Kernel
• Statistically-derived
• ...

See Anselin & Rey (2014) for an in-detail discussion.

How much of a neighbor?

No neighbors receive zero weight: w_ij = 0

Neighbors, it depends, w_ij can be:

• One w_ij = 1  →  Binary

• Some proportion (0 < w_ij < 1, continuous) which can be a function of:

  • Distance
  • Strength of interaction (e.g. commuting flows, trade, etc.)
  • ...

Choice of W

Should be based on and reflect the underlying channels of interaction for the question at hand.

Examples:

• Processes propagated by inmediate contact (e.g. disease contagion)  →  Contiguity weights
• Accessibility  →  Distance weights
• Effects of county differences in laws  →  Block weights

Do your own (contiguity) weights time!

Standardization

In some applications (e.g. spatial autocorrelation) it is common to standardize W

The most widely used standardization is row-based: divide every element by the sum of the row:

$$\bar{w_{ij}} = \dfrac{w_{ij}}{w_{i\cdotp}}$$

where $w_{i\cdotp}$ is the sum of a row.

The spatial lag

The spatial lag

Product of a spatial weights matrix W and a given variably Y

Y_sl = WY

y_sl − i = ∑_jw_ijy_j

• Measure that captures the behaviour of a variable in the neighborhood of a given observation i.
• If W is standardized, the spatial lag is the average value of the variable in the neighborhood

• Common way to introduce space formally in a statistical framework

• Heavily used in both ESDA and spatial regression to delineate neighborhoods. Examples:

  • Moran's I
  • LISAs
  • Spatial models (lag, error...)

Moran Plot

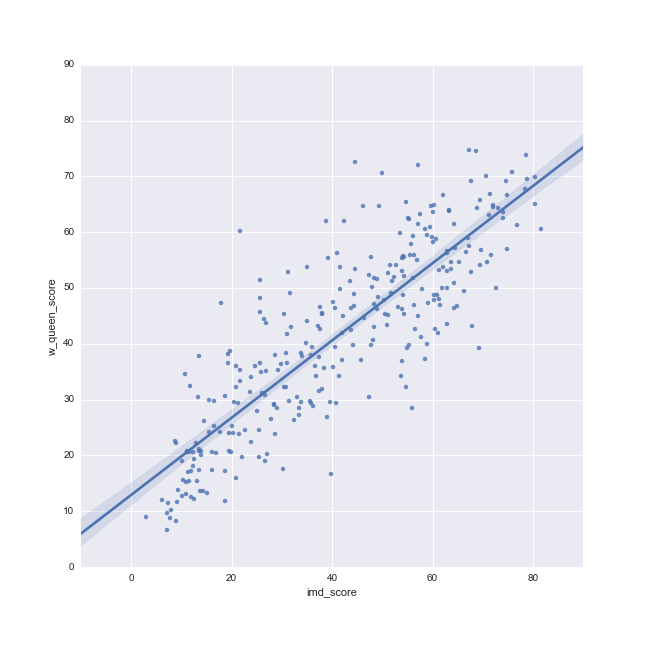
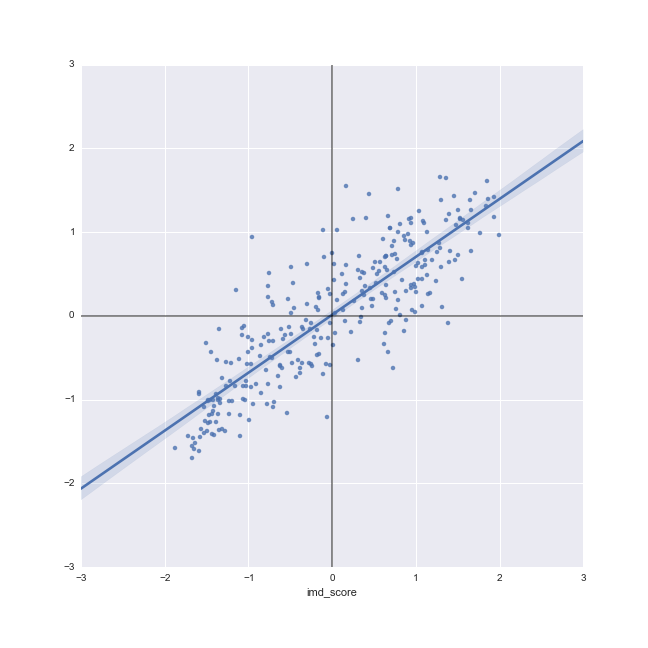
Moran Plot

• Graphical device that displays a variable on the horizontal axis against its spatial lag on the vertical one
• Usually, variables are standardized ($\dfrac{y - mean(y)}{std(y)}$), which divides the space into quadrants
• Tool to start exploring spatial autocorrelation

Moran Plot

Recapitulation

• Spatial Weights matrices: matrix encapsulation of space
• Different types for different cases
• Useful in many contexts, like the spatial lag and Moran plot, but also many other things!